Symbols and Notations
Symbols for these types of questions stand for mathematical operations like +, –, ×, ÷, > , <, ³, £, = and #. So, the students must replace the symbols by mathematical operations and apply the BODMAS’ rule to find the value of the given expression. Other symbols which can be used are DÑ, *, @, $, etc, with proper definitions. Some examples are given belowExample 1: If ‘+’ means ‘–’, ‘–’ means ‘×’, ‘×’ means ‘÷’, and ‘÷’ mean ‘+’ then 15 × 3 ÷ 15 + 5 – 2 = ?
- 0
- 10
- 20
- 6
- None of these
after changing the signs = 15 ÷ 3 + 15 – 5 × 2 = 5 + 15 – 10 =10
Example 2: If 2 * 3 = 12, 3 * 4 = 20 and 4 * 5 = 30, then 2 * 6 is
- 18
- 12
- 21
- 24
- None of these
Example 3: If x $ y = (x + y + xy –1) (x + y + xy + 1), then the value of (4 $ 10) is
- 2915
- 2195
- 2951
- 2955
- None of these
Example 4: If * means “is greater than”, @ means `is less than’; and $ means “is equal to” and if a $ b and b @ c, then
- c * b
- b * c
- c * a
- Both 1 and 3
- None of these
Geometrical Figures
These figures will be divided and subdivided into a number of parts, each part is filled with a number or a letter except one part. The numbers or the letters in the figures follow certain pattern. The objective is to identify the pattern and find the missing number or letter. The problems based on geometrical figures are of various types:Type 1
Based on circles: In these type of, three circles with numbers outside the circle will be given. In the first two circles, the number inside the circle is written according to a particular pattern. The objective of the student is to find the missing number of third circle.
- 7.16
- 9.25
- 6.23
- 8.33
- None of these

- 14
- 10
- 6
- 4
- None of these

Type 2
Circle divided into parts: In such questions, circle is divided into three parts. An arithmetic operation on the numbers gives the missing number.
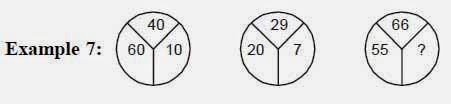
- 2
- 11
- 33
- 44
- None of these
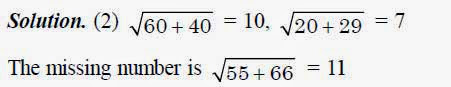

- 9
- 6
- 8
- 4
- None of these
The missing number is (20 – 18)2 = 4
Type 3
Problems based on triangles: In such questions, three triangles are given with numbers inside and outside. The number inside the triangle is obtained by operating some arithmetic operators on the numbers outside the triangle.

- 2
- 1
- 0
- 3
- None of these
The missing number is (1 + 2 + 1) ÷ 4 = 1.
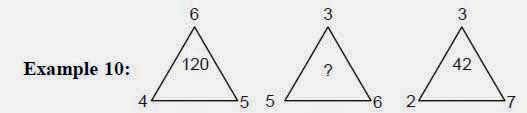
- 70
- 80
- 90
- 1
- None of these
The missing number is (5 × 6 × 3) = 90
Type 4
Problems based on squares: Such questions consist of three squares with five numbers inside the square of the 5 numbers, 4 numbers are at the four corners of the square and one middle number follow some arithmetic operation.

- 4
- 6
- 5
- 7
- None of these
Type 5
Problems based on matrix: In such questions, a square divided into nine parts, three rows and three columns, out of the nine parts, eight parts are filled with one part left vacant. The students need to apply some arithmetic operation to find out the missing number.

- 8
- 9
- 13
- 12
- None of these
Solution. (4) (6 + 1) = 7, (4 + 2) = 6. The missing number = 7 + 5 = 12
No comments:
Post a Comment